Circles are very special – more so than rectangles. Rectangles, you see, come in many different sizes (big, small, enormous etc) and also in many different shapes (tall and thin, short and stubby, square etc).
Circles also come in many different sizes (big, small, enormous etc.) but unlike rectangles, all circles are exactly the same shape. That’s right: even if two circles have different circumference (the distance all the way around the outside) and different diameter (the distance across the middle from one side to the other) the two will always be in the same ratio. This ratio of C/D (circumference divided by diameter) always gives the number
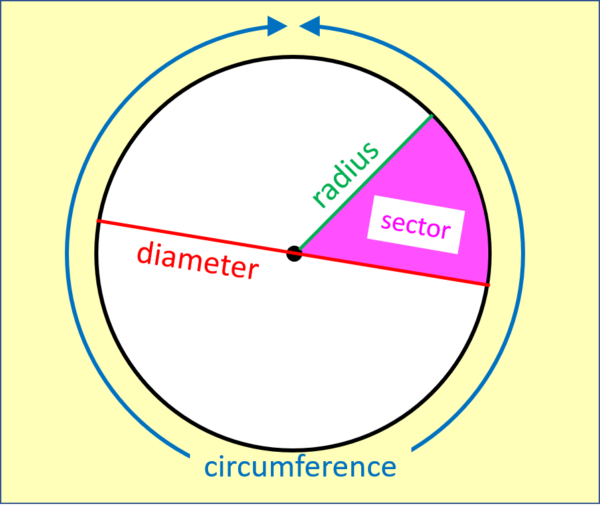
Yes! Find any circle – maybe a plate, the end of a thick candle, or the circle at the top of the kitchen bin. Measure the circumference and the diameter, and you will find the circumference is always 3 and a bit times (actually
It turns out that if you write
3.1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 …
But even that’s not exact because decimal pi goes on forever! In fact, if you search through enough digits of
How about a fraction? Amazingly, you can’t write it as a fraction either!
quantitas in quam cum multiflicetur diameter, proveniet circumferencia
Ooh, snappy! Eventually, someone really clever (Welshman William Jones) came up with the symbol
The whole point of numbers is that they allow us to measure things (how many? how big? how hot? how strong? how many likes? etc etc the list goes on forever, just like the digits of
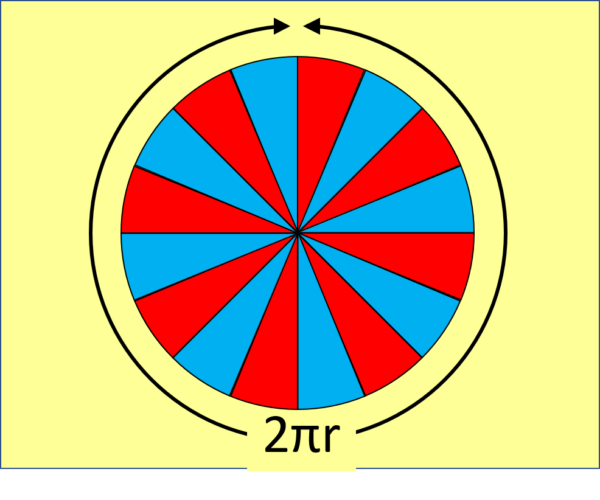
To see how big a circle is, we can cut it up into lots of thin slices (called sectors) like this:
and then rearrange the sectors to make a shape that looks very much like a rectangle, like this:
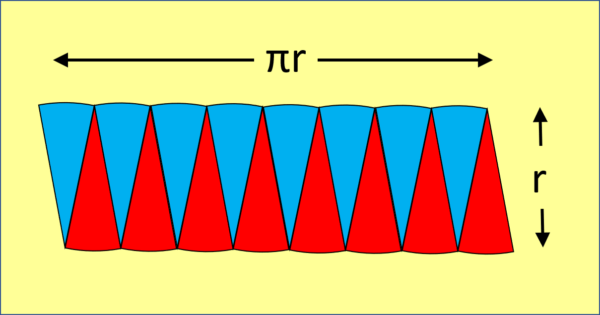
Doing this doesn’t change the area because we’re just rearranging the pieces, we’re not making them bigger or smaller. The height of this “rectangle” is just r – the radius of the circle. The length of the “rectangle” is made up of 8 short arcs, and their total length is just the distance around the original circle, or half the circumference, so half of
Instead of reading this blog, you could have read these two short algebraic formulae instead:
(Algebra, you see, is a great way to say a lot of maths with hardly any writing).
NOTIFY ME OF NEW POSTS BY EMAIL (approx one a month):
[mc4wp_form id=”399″]