07899 756585
FIVE FINGERS: on each hand, with two hands: this is why we count in tens! – starting a new column each time we get to ten in the previous column. One of the simplest ways of keeping count is to use a tally chart: e.g. if you were counting the number of cars of each colour, you would draw one line for each car, then use the fifth line to “close the gate”.
A JOKE FOR YOU!: an ancient Roman walks into a bar, holds up two fingers, and asks “five lemonades, please”.
Do you get the joke? HINT: the ancient Roman symbol for five is the letter V.
PENTAGONS: one of the simplest of the regular polygons, made of five equal sides and five equal angles (each $108^{\circ}$). The famous “Pentagon” building in America is pentagon-shaped with a pentagon-shaped hole in the middle (the hole’s area measures exactly five acres). As well as five sides and five entrances, the building has five floors above ground (plus two basement levels), and five ring corridors on each floor (called A, B, C, D and E).
PENTAGON KNOTS: you can make a perfect pentagon by tying a long thin strip of paper into a knot, then gradually tightening and flattening the knot. Try it!
FIVE POINT GRAPHS: Draw three points on a piece of paper and it’s easy to join each point to each of the other points using curved lines without any of the lines crossing. You can do the same with 4 points too BUT it’s impossible to connect each of five points to each of the others without the lines crossing. Go ahead: try it! (In advanced maths we would say that K3 and K4 are planar, but K5 is not).
PENTOMINOES: this is the word for any flat shape made up of five squares joined together along their sides (in the same way that a domino is made of just two squares joined together). There are twelve different ones (counting shapes that are the same by rotations or reflections as the same). Grab some paper and see how many of them you can find! Two are shown on the image at the start of this post.
PENTAGRAMS: Connect each corner of a pentagon to each of the other corners and you have a pentagram (five pointed star).
ATTENTION: this last bit is quite hard – read on if you dare!
The diagonal of a unit square (all sides are of length 1 unit) has length $\sqrt{2}$ units (you can prove this using Pythagoras Theorem). But what about the diagonal of a unit pentagon? It turns out to be the Golden Ratio $\frac{1+\sqrt{5}}{2}$ – a number with all sorts of interesting properties. Here’s a sketch of how to prove this result:
GOLDEN RATIO PROOF:
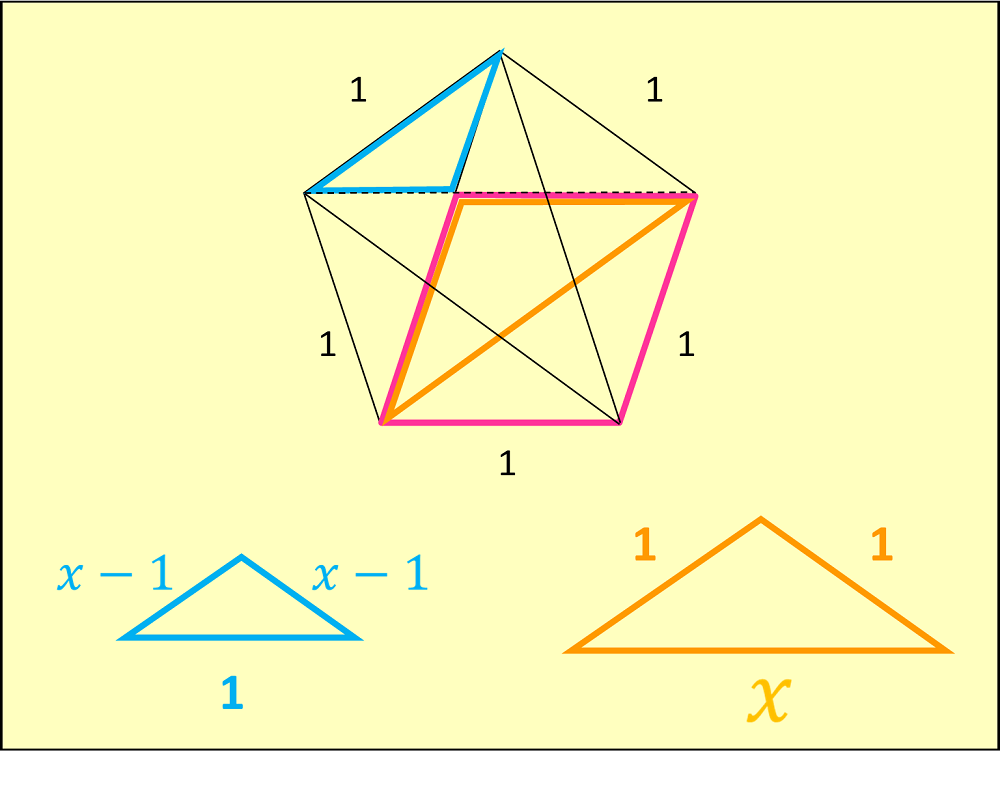
All the sides of the pentagon have length one, and suppose each diagonal (between two non-adjacent corners) is of length $x$ units.
In this picture, note that the pink shape is a rhombus (four equal sides).
Note also that the blue and red triangles are similar (same shape but different size).
Drawing these two triangles out side by side (and rotating so they’re both the same way round), the lengths are all as shows. The $x-1$ is because it’s a diagonal subtract the pink length (the pink length = 1 same as each side of the pentagon – because the pink shape is a rhombus).
The length scale factor (what you multiply by to get from little to big triangle) is $x/1$ (by comparing the bases) but it’s also $1/(x-1)$ (by comparing the sloping sides).
Equating these we get:
$\Large{\frac{x}{1} = \frac{1}{x-1}}$
Cross-multiply to remove the denominators and rearrange to get a quadratic equation whose solution is the Golden Ratio $\Huge{\frac{1+\sqrt{5}}{2}}$
IF YOU’VE ENJOYED THIS POST: see also what’s special about the number three? , what’s special about the number 1 , what’s special about the number two and what’s special about the number ninety-one?.