A WARM-UP: Quickly: is 91 a prime number or not?
Don’t think too hard, just your gut feeling: yes or no? I’ll return to this later, but first:
NINETY-ONE IS A TRIANGULAR NUMBER:
The Triangular numbers 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, … come up in lots of places, but at their simplest they are the number of snooker balls you would need for a triangle with, in this case 13 rows. Ninety-one is triangular because 91=1+2+3+4+5+6+7+8+9+10+11+12+13. So we could use the notation

NINETY-ONE IS A SQUARE-BASED-PYRAMID NUMBER:
The SQUARE PYRAMIDAL NUMBERS 1, 5, 14, 30, 55, 91, … are the number of cannonballs you would need in a stack of nested squares with, in this case 6 rows. Ninety-one is Square-Based-Pyramidal because
So we could use the notation 
Interesting, don’t you think, that 91 is both triangular and pyramidal number? Amazingly it has been proven that the only other numbers with this property are 1, 55, and… wait for it … 208335. I find that fact AMAAAAZING!
BUT IS IT PRIME?
Well, 2 doesn’t go into it, neither does 3 or 5. It doesn’t appear in any of the times tables (up to 12×12), so it certainly looks prime at first glance. However, it is NOT prime, because 91=7×13. If you compare the rectangular image below with the triangular one above, you can see how to rearrange the 91 snooker balls into a 7×13 rectangle.
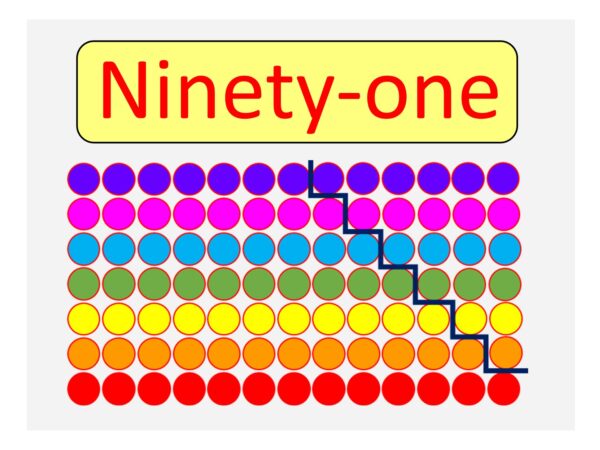
This trick of rearranging the snooker balls in a big triangle to make a rectangle works for all the triangular numbers, so none of the triangular numbers (except for 3) are prime – they are all composite (meaning “not prime”).
ONE LAST TRICK:
91 also features in the following puzzle: what number comes next in this sequence? Can you see the answer? It’s very silly: if you can’t see it then try viewing the image upside down!
